Article-Journal

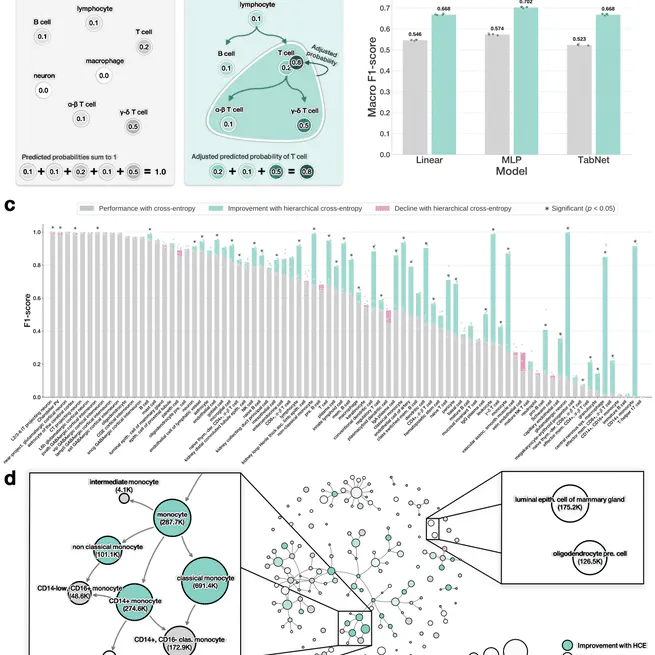
Accurately annotating cell types is essential for extracting biological insight from single-cell RNA-seq data. Although cell types are naturally organized into hierarchical ontologies, most computational models do not explicitly incorporate this structure into their training objectives. We introduce a hierarchical cross-entropy loss that aligns model objectives with biological structure. Applied to architectures ranging from linear models to transformers, this simple modification significantly improves out-of-distribution performance (12–15%) without added computational cost.

Apr 23, 2025

Among the properties describing the behavior of centrality measures with respect to network modifications, score monotonicity means that adding an arc increases the centrality score of the target of the arc; rank monotonicity means that adding an arc improves the importance of the target with respect to the remaining nodes. It is known that score and rank monotonicity hold in directed graphs for almost all the classical centrality measures. In undirected graphs one expects that the corresponding properties hold when adding a new edge—in this case, both endpoints of the new edge should enjoy the increase in score/rank. However, recent results have shown that this is not true: for many centrality measures, it is possible to find situations in which adding an edge reduces the rank of one of its two endpoints. In this paper we introduce a weaker property for undirected networks, semi-monotonicity, in which just one of the two endpoints of a new edge is required to enjoy score or rank monotonicity. We show that this property is satisfied by closeness centrality, by a large class of distance-based centralities, and (somehow surprisingly) by betweenness centrality. In the last two cases, we prove in fact a stronger property, basin dominance, which is of independent interest.

Sep 1, 2024